H2PTM (2005) Leleu-Merviel
La structure du Aha.
De la fulgurance comme une percolation
|
Sommaire
- 1 Introduction
- 2 Les quatre phases du processus créatif
- 3 Théorie de la percolation (PT)
- 4 Application de la PT aux réseaux de communication
- 5 Contribution de la PT à la description du processus créatif
- 5.1 Fragmentation de la connaissance
- 5.2 Mise en œuvre de la Théorie de la percolation
- 5.3 Commentaires et perspectives
- 6 Conclusion
- 7 Bibliographie
- Résumé
- Le processus inventif est souvent décomposé en quatre périodes distinctes. La plupart des inventeurs ont évoqué l'évidence aveuglante avec laquelle l'idée novatrice surgit tout à coup au cours de la phase 3. Certains emploient le terme d'illumination. Les anglo-saxons l'appellent le Aha. Le concept de fulgurance est retenu ici. Néanmoins, si le phénomène est connu, on dispose de peu d'explications quant à ce qu'il s'y produit réellement. Ce papier se fonde sur l'hypothèse que la théorie de la percolation en fournit un modèle pertinent. Il en résulte une interprétation du processus inventif à partir de laquelle il est possible d'inférer la place que peut y tenir l'outil numérique ainsi que les moyens de favoriser l'émergence créative. Les résultats peuvent être étendus aux processus cognitifs en général et permettent d'expliquer notamment la dissonance cognitive.
- Mots-clés
- cognition, sens, signification, représentation, manipulation de données, traitement de l'information.
- Abstract
- The inventive process is often decomposed into four distinct periods. Most inventors speak of the blinding obviousness with which innovative ideas suddenly burst out in phase 3. Some use the term of illumination, or also called the a-h-a (the Eureka cry) phenomena. It is here that the concept of a "cognitive lightening flash" (fulgurance) is proposed. That said, even if the phenomenon is known, we have little explanation about what really occurs. With this is mind, the paper is based on the hypothesis that the theory of percolation provides a relevant model. It offers an interpretation of the inventive process from which it is possible to infer the role of the digital tool as well as ways to facilitate the emergence of creativity. The results can be extended to cognitive processes in general and explain, notably, cognitive dissonance.
- Keywords
- cognition, meaning, signification, representation, manipulation of data, information processing.
Introduction
À l'heure où le formidable foisonnement technologique a fait de la machine numérique un partenaire fiable de créativité, nous promettant l’accession à toutes les fantaisies jamais imaginées, il n’est pas inopportun de s’interroger quant au « processus créatif » en lui-même. Si créer devient une ambition techniquement plus accessible que jamais, mieux comprendre « ce que créer veut dire » ne peut que favoriser l’émergence créative.
Se pose notamment de façon accrue la question de la créativité humaine, de ses spécificités, de ses principes, de ses modes de fonctionnement, vis-à-vis de la machine et de ses apports propres en ce domaine.
Ce papier envisage globalement le « processus inventif », sans faire de différence majeure entre la création artistique ou la découverte de nouveaux modèles scientifiques, ainsi qu’y engage par exemple Howard Gardner dans son ouvrage Les formes de la créativité (Gardner, 1993/2001). Il appelle en effet à considérer que ce sont des formes diverses d’intelligence qui se manifestent parmi les sept qu’il a identifiées (Gardner, 1983/1997), sans qu’une distinction ne s’impose dans le processus inventif par lui-même.
Les quatre phases du processus créatif
Certains travaux se sont attachés à décrire le processus créatif (Rouquette, 1997). (Wallas, 1926) est le premier d’entre eux à identifier quatre phases distinctes par lesquelles passe successivement le parcours du créateur. La présentation succincte ci-dessous effectue une synthèse entre (Wallas, 1926) et (Jaoui, 1996), empruntant à l’un ses appellations et à l’autre ses descriptions.
L'imprégnation
Au cours de la première période, appelée phase d’imprégnation, l’inventeur rassemble un très grand nombre de données, d’observations, de documentation, de connaissance, d’information. Cette étape est à la fois active et passive puisque l’inventeur opère une démarche volontaire de recherche de documents, mais en même temps il s’en laisse imprégner, il les absorbe comme une éponge.
L’incubation
Selon Hubert Jaoui : « La phase d’incubation est à dominante inconsciente. Le sujet porte en lui l’objet de sa recherche comme une femme porte en elle l’oeuf fécondé qui deviendra l’embryon et, un jour, le “rejeton”. Avec cette différence qu’ici le cycle de gestation n’est pas prévisible et qu’il peut durer de quelques minutes à quelques années ou davantage : certains inventeurs sont morts avant d’avoir accouché de leur idée » (Jaoui, 1996).
L’illumination
Quand tout se passe bien, l’accouchement donne naissance à l’idée novatrice. Hubert Jaoui, de nouveau, indique : « On emploie couramment le terme d’illumination. La plupart des inventeurs ont en effet parlé de l’évidence aveuglante avec laquelle l’idée leur apparaissait. Un moment avant, ils étaient encore dans l’obscurité, et soudain, comme un éclair éblouissant dans un ciel noir, l’idée leur apparaît sous une forme pratiquement achevée » (Jaoui, 1996).
La vérification
La phase de validation est impérative après l’illumination, car il reste à vérifier que l’idée trouvée est pertinente. Dans le cas d’une création artistique ou littéraire, c’est le jugement esthétique du créateur lui-même, de son environnement, puis plus tard de la critique et enfin du public qui établit le caractère novateur de la production. Dans le cas d’une découverte scientifique, la vérification est établie par expérimentation, par recoupements, par répétition d’observations concluantes avant que les résultats ne soient présentés aux pairs afin qu’ils les valident et les reconnaissent. Dans l’entreprise, il s’agit de transformer l’invention en innovation, par la mise en application. Il s’avère souvent nécessaire d’effectuer un transfert, c’est-à-dire passer le relais de l’inventeur aux innovateurs, qui sont avant tout d’excellents communicants, capables de faire reconnaître la valeur de l’idée nouvelle aux personnes chargées de la réaliser, de l’appliquer, de la valoriser et de la vendre. En outre, l’inventeur est parfois tenté d’arrêter sa démarche à la production de l’idée. C’est la plainte fameuse du cinéaste René Clair : « Mon film est fini. Il n’y a plus qu’à le faire ».
Dans tous les cas, la vérification constitue une phase plus applicative, moins créative, plus modeste, et notablement plus longue.
La fulgurance
S’il existe des outils connus pour structurer le travail à accomplir au cours de la phase de recherche documentaire, si le protocole de vérification est le plus rigoureux et le plus formalisé, les deux étapes centrales demeurent relativement mystérieuses. On dispose en effet de peu d’explications quant à ce qu’il s’y produit réellement.
Le phénomène d’illumination, notamment, est intrigant. Tous les témoignages concordent sur sa description. Les anglo-saxons l’appellent le Aha (Akin, 1996) et le désignent également par le terme insight. Il coïncide avec le célèbre cri d’Archimède : Eurêka ! Il n’est pas si éloigné du « Ça y est, j’ai compris ! » de nos étudiants. Certains le désignent comme un « flash » ou une inspiration, voire une révélation.
« Les désarrois des Maîtres du sens à l’ère numérique » présenté à H2PTM’03 (Leleu-Merviel, 2003) indiquait déjà que cette mécanique d’émergence subite est désignée par Michel Vinaver comme une fulgurance (rencontre fortuite faisant soudainement sens () cité dans (Pavis, 2002)), laquelle fait surgir brusquement l’ampleur d’une « signifiance » extrêmement puissante. Parmi tous les autres, c’est ce terme, dénué de toute connotation métaphysique ou mystique, que nous retiendrons préférentiellement pour la suite.
Théorie de la percolation (PT)
L’hypothèse développée ici est que la théorie de la percolation fournit un modèle pertinent pour décrire la fulgurance.
Mécanisme de la percolation
La Théorie de la Percolation (PT) est l’un des modèles chaotiques les plus simples pour représenter les systèmes désordonnés.
Définition : le terme percolation vient du latin percolatio qui signifie filtration.
Employé dans un grand nombre de situations, il évoque les notions de propagation et agglutination dans les environnements aléatoires partiellement interconnectés.
Définition : un percolateur est une machine à café qui permet d’ajuster la force du café désiré en pressant le mécanisme de filtrage pour le maintenir plus ou moins serré. Quand la pression augmente à l'intérieur du filtre, la densité du marc de café augmente à proportion en raison de l'agglutination des fines particules de café.
Définition : cependant, il existe une densité limite. Au-delà d’une valeur limite donnée, l’eau ne peut plus s’écouler à travers la poudre de café. Cette densité limite est appelée le seuil de percolation.
Le problème formel consiste à décrire l'agglutination des particules de café en liaison avec la densité du marc de café, et à caractériser la propagation de l’eau à travers ce milieu aléatoire et non homogène (Lesne, 1996). Ce phénomène peut être représenté par le biais d’un réseau de canaux entre les particules de café. Chaque canal est alors aléatoirement ouvert ou fermé (Zallen, 1983). Quand la densité augmente, davantage de canaux sont fermés et l’eau traverse avec plus de difficulté. Le seuil de percolation est atteint lorsqu’il n’existe plus de chemin permettant l’écoulement de l’eau le long des canaux ouverts.
Exemples de modélisations par la PT
La Théorie de la Percolation (PT) trouve désormais de nombreux champs d’application. Quelques-uns d’entre eux sont rapidement évoqués ci-dessous.
Transition d’un archipel insulaire à un continent
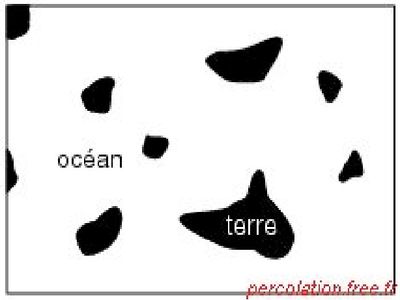
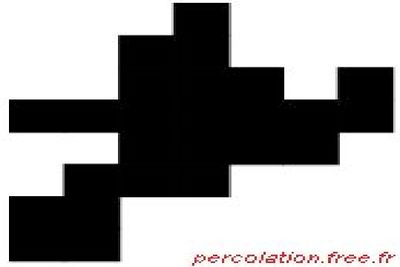
Sur la figure 1 ci-dessous (Pajot, 2001), on constate qu’un naufragé initialement sur l’une des îles de l’archipel et ne disposant pas de moyen de se déplacer sur ou dans l’eau (il n’a plus de bateau et ne sait pas nager) reste sur cette première île, dans la mesure où il lui est impossible de marcher sur l’eau.
Quand le niveau de l’océan décroît, la surface des îles augmente et certaines d’entre elles se rejoignent, comme on le voit sur la figure 2. Le naufragé n’est plus prisonnier : il peut se déplacer entre les îles interconnectées.
Quand le niveau de l’océan atteint une certaine valeur seuil, apparaît un continent comportant un grand nombre de lacs, mais où le naufragé peut traverser sans plus rencontrer de barrière maritime.
Ce modèle a été proposé également pour représenter la propagation des incendies en forêt (De Gennes, 1976).
Transition entre isolant et conducteur
Le modèle de la percolation a évidemment été employé en physique et en chimie.
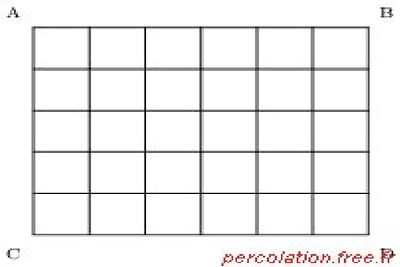
Considérons par exemple une grille carrée dont chaque nœud est aléatoirement occupé avec la probabilité p ou vide avec la probabilité 1-p. Pour simplifier, supposons que les nœuds occupés représentent des conducteurs électriques et les nœuds vides des isolants. Le courant électrique peut en outre circuler entre nœuds conducteurs contigus. Pour les faibles valeurs de p, les nœuds conducteurs sont isolés ou forment de petits amas de nœuds contigus. Deux nœuds conducteurs appartiennent au même amas s’il existe un chemin entre conducteurs contigus qui les connecte l’un à l’autre et que donc un courant peut circuler entre eux. Ainsi, pour les faibles valeurs de p, la construction est isolante, puisqu’un chemin conducteur connectant les bords opposés de la grille n’existe pas. Au contraire, pour les valeurs élevées de p, il existe beaucoup de chemins conducteurs d’un bord de la grille à l’autre, le courant circule et la construction est conductrice. De ce fait, aux valeurs intermédiaires, il existe nécessairement une valeur seuil pc, où pour la première fois le courant électrique peut percoler d’un bord à l’autre de la grille. En dessous de pc, on est en présence d’un isolant ; au-dessus de pc, il s’agit d’un conducteur. La valeur limite est appelée le seuil de percolation ou, comme elle sépare deux phases différentes, le seuil critique.
Application de la PT aux réseaux de communication
Les quelques exemples précédents ont montré l’application de la Théorie de la Percolation à des domaines scientifiques variés (sciences de la terre, sciences physiques, etc...). Son emploi amène également des ressources nouvelles dans l’étude des réseaux de communication.
Défaillances dans les réseaux de communication
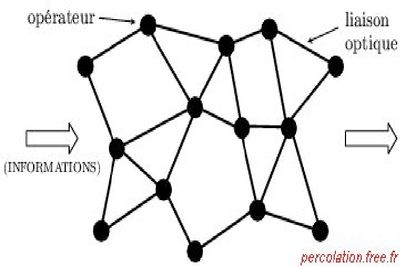
Considérons un réseau de communication composé de n sites. Chaque site est relié à ses voisins par des liaisons (par exemple optiques) dont l’efficience est p-aléatoire.
Percolation de liens
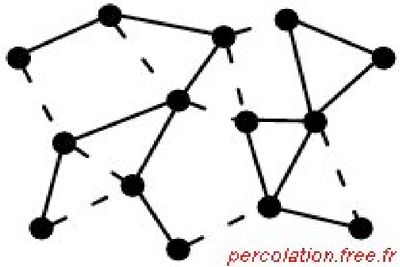
Supposons qu’une proportion 1-p de liaisons existantes sont détruites aléatoirement, pour différentes raisons (maintenance insuffisante, réparations défectueuses, actes isolés de sabotage, défaillances diverses, dérangement ou blocage, etc.).
Percolation de sites
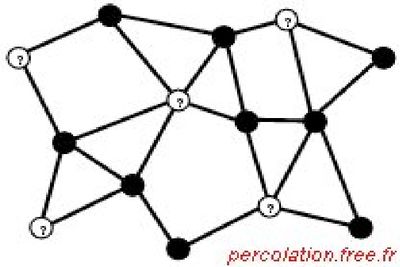
Il peut se produire que les liaisons soient 100% efficaces, mais qu’il existe un risque sur les sites avec une probabilité de p. Dans ce cas, on parlera d’une percolation de sites.
Percolation de sites et de liens
Finalement, on se trouve en présence d’une percolation de sites et de liens lorsque les sites et leurs liaisons sont aléatoirement dégradés en même temps.
Cas des sciences humaines et sociales
Dans le champ des sciences humaines et sociales, l’approche interdisciplinaire intégrant les sciences de la complexité, qui a émergé récemment, a ouvert des voies pour décrire ce type de problème grâce à un large éventail d’outils théoriques parmi lesquels figure la Théorie de la Percolation.
Dans ce cas, le réseau sous-jacent sur lequel s’effectue la percolation est le réseau des acteurs sociaux, tandis que les liens représentent les interactions entre ces acteurs. Dans ce cadre, des résultats significatifs ont été obtenus, comme l’explication des comportements des marchés de diffusion les plus extrêmes, proches de 0% ou 100%, dans l’industrie des médias. Une approche similaire peut être employée pour modéliser la diffusion des nouvelles idées ou des nouvelles croyances (Chitea, 2004).
Représentations formelles de la PT
De façon plus formelle, les mathématiciens considèrent une grille de points. Il s’agit d’une matrice infinie de points discrets dont l’arrangement et l’orientation apparaissent exactement semblables quel que soit le point d’où la matrice est vue. On peut observer que la matrice de la figure 8 remplit ces conditions.
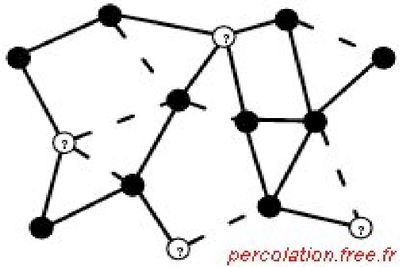
La figure suivante illustre alors un modèle de percolation de sites,
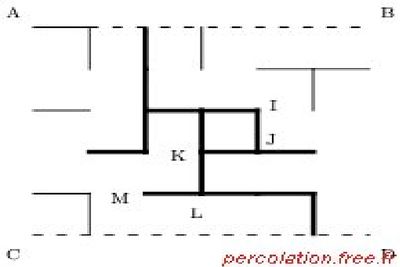
tandis que la figure 10 propose un modèle formel de la percolation de liens.
Contribution de la PT à la description du processus créatif
Nous allons maintenant montrer comment la Théorie de la Percolation peut être mise en oeuvre pour appréhender le processus créatif.
Fragmentation de la connaissance
Çà et là apparaît dans la littérature la notion d’unité élémentaire de connaissance. Certains parlent d’unité d’information (Balpe, 1990), d’autres de brique (Ranwez, 1999). Nous retiendrons le terme de fragment : il désigne une parcelle granulaire de connaissance, homogène et cohérente, qui peut être isolée conceptuellement et associée à d’autres fragments granulaires.
Adopter cette notion équivaut à admettre que la connaissance n’est pas continue. Ainsi, il est possible de la structurer en discrétisant son contenu en un ensemble de parcelles granulaires ou fragments. A ce point de la réflexion, nous ne précisons nullement la dimension des fragments, qui peuvent être plus ou moins volumineux en fonction de la granularité retenue pour la décomposition. Cet aspect de la question n’influence pas la suite du raisonnement : nous ne l’évoquerons donc pas.
Ce qui est plus déterminant, c’est de noter que les fragments ne correspondent pas seulement à des amas de données déclaratives, mais qu’ils peuvent également inclure des descriptions procédurales.
Mise en œuvre de la Théorie de la percolation
Voyons comment cette définition liminaire permet de mettre en œuvre la Théorie de la Percolation.
Divers modèles de la pensée
Deux grands courants s’affrontent dans les sciences cognitives : le symbolisme et le connexionnisme. Le symbolisme suppose un traitement sériel où chaque étape du traitement de l’information est gérée par un module spécialisé. Le traitement de l’information y ressemble à un programme informatique consistant en manipulation de symboles selon des règles logiques. Au contraire, l’hypothèse connexionniste fonde l’étude de la pensée non plus sur la manipulation de symboles, mais sur la structure des neurones et leur enchevêtrement. Les unités de traitement, mobilisables en parallèle, sont toutes connectées entre elles, formant ainsi un vaste réseau dans tout le cerveau.
Toutefois ces deux approches, longtemps opposées, convergent aujourd’hui dans certains modèles, comme le modèle de la mémoire de McClelland (McClelland, 1995) qui les conjugue, chacun prenant en charge un niveau de fonctionnement différent, global ou local.
Définition de la connaissance globale comme un réseau entre fragments
Conformément à ce type de conception hybride, considérons à présent l’hypothèse selon laquelle la connaissance globale définit un réseau dans le cerveau, où les sites sont les fragments de connaissance connectés (ou non connectés) par des liaisons p-efficientes.
Alors, résoudre tout type de problème (résolution d’un problème mathématique, problème de création, recherche d’une idée nouvelle, problème de management, problème pratique, ...) peut être assimilé au passage de la position initiale (hypothèses, faits initiaux, visées du projet...) à une position finale où le problème est considéré comme résolu.
Analogie avec les représentations PT
Dès lors que la résolution de problème (l’invention d’une solution) a été posée comme la découverte d’un chemin entre deux sites distants, reliés directement ou indirectement, apparaît immédiatement l’analogie avec les descriptions de défaillances dans les réseaux de communication, présentées dans la partie 4 et illustrées par les figures 4 à 7.
Par ailleurs, en posant que la position initiale correspond à un bord d’une matrice carrée et la position finale au bord opposé, alors la résolution du problème (s’appuyant implicitement sur des connaissances) équivaut à la traversée d’un bord à l’autre de la matrice. Dès lors, les figures 8 à 10 sont pertinentes également.
Résultats obtenus grâce à la modélisation par la PT
En utilisant les principes de la Théorie de la Percolation, on en déduit donc que l’établissement de ce chemin n’est possible que s’il existe un grand nombre de fragments de connaissance en liaison d’un bord au bord opposé, et si p est supérieur ou égal à la valeur critique pc. En dessous de cette valeur, il est impossible de construire un chemin qui traverse les fragments de connaissance.
PT, modèle pertinent du processus inventif
Comme nous l’avons indiqué en préambule, nous ne faisons pas de différence majeure entre la résolution d’un problème et l’invention novatrice. Par conséquent, à l’aide de la Théorie de la Percolation, nous pouvons désormais interpréter les 4 phases du processus inventif présentées au paragraphe 2.
Imprégnation
L’imprégnation correspond au dépôt des fragments granulaires dans la matrice de structure de la connaissance.
Incubation
L’incubation, dont la nature demeurait jusque-là très mystérieuse, serait alors la construction d’une organisation structurée par le réseau des liaisons entre fragments, un paramètre de p-efficience adéquat étant affecté à chacune des liaisons.
Fulgurance
La fulgurance n’est plus alors que le moment précis où la valeur croissante de p atteint le seuil critique de percolation pc. Brusquement et pour la première fois, un chemin est établi via un amas percolant entre les deux bords de la matrice représentative du problème à résoudre. Une percolation entre les données se produit alors.
Résultats concrets
De tout ceci, il résulte qu’il existe trois opérations à accomplir pour augmenter le potentiel inventif :
- Ajouter de nouveaux fragments dans la matrice de structure de connaissance.
- Ajouter de nouvelles liaisons entre fragments pour augmenter la taille des amas percolants.
- Augmenter la p-efficience de l’ensemble des liaisons pour passer au-dessus de la valeur seuil pc.
Le premier résultat important est sans doute qu’il ne suffit pas d’une grande accumulation de fragments granulaires de connaissance. Il faut aussi que ces fragments soient connectés par des liaisons. Les liaisons s’avèrent finalement plus importantes que les fragments eux-mêmes. Car non seulement les liaisons doivent impérativement exister, mais elles doivent de plus être suffisamment efficientes pour percoler, sinon les fragments sont inutiles.
Commentaires et perspectives
Le raisonnement tel qu’il a été présenté ci-dessus appelle quelques commentaires à même d’ouvrir des perspectives pour des approfondissements futurs.
Soutien de l’outil numérique dans l’émergence créative humaine
Dès que nous évoquons la connaissance en termes de réseau constitué de sites reliés par des liens, la similitude avec les systèmes d’information, les hypertextes, les hypermédias et Internet s’impose à l’esprit. Une question émerge alors : l’ordinateur est-il capable d’effectuer des percolations ? Les unités d’information et/ou les fragments sont les composants de base des applications hypermédia. Le World Wide Web offre aujourd’hui une quantité de fragments de connaissance si large et en telle expansion qu’on peut la considérer comme infinie. A ce titre, l’ordinateur est un outil adéquat pour accompagner la phase d’imprégnation.
En outre, certains de ces fragments sont connectés par des liens. Mais le lien informatique est très primitif : il est binaire, il existe ou pas (1 ou 0). Pour s’approcher d’un système percolant, il serait intéressant de développer des systèmes à liens pondérés par une p-efficience. Les questions sont alors d’une autre nature : qu’est-ce que l’efficience ? Existe-t-il une méthode pour l’évaluer ou la mesurer ? Comment attribuer une valeur à p ?
Revenons sur la remarque initiale selon laquelle on sait très peu de choses quant à ce qui se produit dans la phase d’incubation. L’hypothèse percolante fournit des pistes de recherche fécondes à ce propos. Une méthode comme la méthode des cartes mentales (De Brabandere, 2002) contribue à mieux appréhender le mécanisme du lien. Cependant, elle est aussi assez primitive et représente sans doute trop sommairement le perfectionnement du mécanisme humain « d’association d’idées ».
Comme nous l’avons avancé dans (Leleu-Merviel, 2003), la fulgurance relève de mécanismes très élaborés, aujourd’hui peu connus et dont l’un des modèles les plus percutants est fourni par exemple par la théorie de l’intégration conceptuelle de Mark Turner et Gilles Fauconnier (Fauconnier, 2002). Comme la validation et la preuve, elles sont inaccessibles à la machine à ce jour et demeurent spécifiquement humaines.
Liens, liaisons, lictions
L’hypothèse développée ici repose sur la fragmentation de la connaissance en sites discrets reliés par des liens. Néanmoins, le raisonnement général est resté très évasif sur la nature des liens. Le paragraphe précédent a montré que le lien informatique dans l’hypertexte constituait une approximation extrêmement rudimentaire de la liaison nécessaire à un amas percolant.
Ceci rejoint les prémisses des systèmes hypertextes tels que conçus par leurs pères fondateurs (Bush, 1945). Rappelons que dans leur esprit, le système documentaire appelé MEMEX fonctionnait par association, les utilisateurs déposant des liens entre documents. Mais un lien pouvait indifféremment associer des documents traitant d’un même thème, des documents citant un même auteur, ou plus généralement des documents entretenant un rapport quelconque, non nécessairement explicité, mais pourtant significatif pour la personne qui l’a établi. Un tel système visait à dépasser l’indexation documentaire classique, fondée essentiellement sur la caractérisation à partir de champs clefs. La définition même de l’hypertexte est conforme à cette idée puisque Theodor Nelson (Nelson, 1981) le définit comme : « une série de fragments de texte -a series of text chunks- reliés par des liens, proposant au lecteur des parcours différents ». Mais rappelons-nous encore que ces pionniers réfutent l’implémentation qu’en fournit le Web, puisque Theodor Nelson s’insurge : « Beaucoup de gens pensent que Xanadu a été une tentative de construire le World Wide Web. Au contraire : le World Wide Web était exactement ce que nous essayions d’éviter ».
La nature de la liaison reste donc le point central à élucider pour actualiser pleinement le potentiel de l’hypothèse percolante. Dans (Leleu-Merviel, 2004), je proposais une notion de proximité ou de voisinage fondée sur une appréhension topologique de l’espace imaginal des connaissances, la distance entre fragments étant alors une distance sémantique reposant sur certains aspects dont la similarité génèrerait des résonances entre fragments. Deux fragments proches ou voisins seraient alors non pas deux fragments situés dans des unités d’information contiguës dans l’espace des données, mais des fragments que l’on peut rapprocher au regard de certaines propriétés qu’ils partagent.
Mioara Mugur-Schächter (Mugur-Schächter, 2005), dans sa Method of Relativized Conceptualization, évoque des « cohérences de voisinage », des « attractions sémantiques par continuité sur les bords des événements élémentaires » sur la base d’aspects qui composent la structure qualificationnelle de la connaissance communicable. Désignons désormais par le terme liction cette espèce d’attraction qualifiée par la continuité de certains aspects.
Des travaux futurs s’attacheront à approfondir ces notions pour tenter de mieux cerner le processus humain de conceptualisation, seul à même de permettre l’opérationnalisation de ce que nous n’appelons plus ni le lien, ni la liaison, mais la liction.
Application dans le contexte pédagogique
Nous avons admis que le processus d’invention créative, de découverte, était assez semblable au processus d’acquisition de connaissances nouvelles. Les résultats obtenus par l’hypothèse percolante peuvent donc être étendus aux processus cognitifs en général. Ils permettent d’éclaircir certaines difficultés que le pédagogue rencontre parfois, et qu’il est contraint de résoudre de façon intuitive, sans savoir très bien si cela « fonctionne ».
Par exemple, il arrive que les apprenants ne parviennent pas à résoudre un problème donné alors qu’ils possèdent assurément les connaissances nécessaires pour ce faire (cas très fréquent d’étudiants en difficulté sur des travaux dirigés ou des travaux pratiques en application d’un cours parfaitement assimilé, parfois depuis longtemps). Ce diagnostic indique clairement que des liaisons manquent, ou que l’efficience entre liaisons est insuffisante. Dans ce cas, il faut donc accroître les liaisons et leur efficience. Ajouter de nouveaux fragments de connaissance s’avère parfaitement inutile, voire contre-productif.
D’autres cas peuvent faire apparaître une dissonance cognitive (Festinger, 1957). Cela signifie que le canal de liaison entre sites voisins est définitivement fermé et que la valeur de p-efficience est égale à 0. Il est alors impossible de réouvrir le canal directement, car l’apprenant croit que c’est impossible : là réside précisément la définition de la dissonance cognitive. On cite souvent en exemple le cas de cette formation aux nouvelles techniques de découpe du métal, où les étudiants n’avaient pu admettre le principe de la découpe à l’eau sous pression, car l’eau éteint le feu, seul apte à découper le métal à leurs yeux. Il convient alors de contourner la difficulté en trouvant un nouveau chemin entre les deux sites via des détours et des relais. C’est le seul moyen de faire diversion, parvenir à la compréhension et vaincre la difficulté.
Conclusion
L’analyse présentée ici s’est fondée sur l’hypothèse que la connaissance est constituée en réseau dans le cerveau humain, où les sites sont des fragments discrets de connaissance connectés (ou non-connectés) par des lictions p-efficientes. Ceci permet de mettre en œuvre la Théorie de la Percolation pour modéliser la façon dont notre esprit mobilise ces fragments afin de résoudre un problème (en s’appuyant implicitement sur cette connaissance). Pour recourir à cette méthode, trois hypothèses doivent nécessairement être vérifiées :
- Le phénomène s’inscrit dans un espace contenant un très grand nombre d’éléments,
- La liction entre éléments est fondée sur une propriété de l’ordre du voisinage, de la contiguïté ou d’un autre aspect rendant compte d’une forme de proximité sémantique,
- Cette relation entre éléments peut être caractérisée de façon aléatoire.
L’hypothèse percolante permet alors (et pour la première fois) d’approcher ce qui peut se produire lors de la fulgurance. La percolation y définit alors un changement d’état, une transition de phase. Elle montre que dans le processus inventif, la machine numérique fournit une aide efficace aux phases 1 et 2, mais que les deux suivantes demeurent fondamentalement du ressort de l’humain.
Cependant, cette proposition n’est à ce stade pas plus qu’une conjecture en abyme, une fulgurance quant à la fulgurance. La quatrième phase, celle de la validation, nécessite des expérimentations permettant par recoupements d’aboutir à des observations concluantes. En particulier, la nature des lictions entre fragments doit être mieux cernée afin de pouvoir prouver que l’augmentation de leur nombre et l’accroissement de leur p-efficience favorise l’émergence créative. Seul ce travail doit permettre d’attester que la piste originale présentée ici est féconde.
Bibliographie
[Akin, 1996] ↑ Akin Ö. et Akin C., « Frames of reference in architectural design: analysing the hyperacclamation (A-h-a-!) », in Design Studies 17, 1996, pp.341-361.
[Balpe, 1990] ↑ Balpe J.P., « Hyperdocuments, hypertextes, hypermédias », Paris, Eyrolles Sciences,1990.
[Bush, 1945] ↑ Bush V., « As we may think, The atlantic monthly », juillet 1945.
[Chitea, 2004] ↑
Chitea A., « Percolation Theory ».
En ligne : http://www.iubremen.de/course/c02009/32218/ (on line course) (consulté le 4 mai 2004)
[De Brabandere, 2002] ↑ De Brabandere Luc, « Le management des idées. De la créativité à l’innovation », Paris, Dunod, 2002.
[Fauconnier, 2002] ↑ Fauconnier G. et Turner M., « The Way We Think: Conceptual Blending and the Mind’s Hidden Complexities », New York, Basic Books, 2002.
[Festinger, 1957] ↑ Festinger L., « A Theory of Cognitive Dissonance », Stanford (California), Stanford University, 1957.
[Gardner, 1983/1997] ↑ Gardner H., « Les formes de l’intelligence », Paris, Éditions Odile Jacob, 1997. Édition originale : Frames of mind, New York, Basic Books, 1983.
[Gardner, 1993/2001] ↑ Gardner H., « Les formes de la créativité », Paris, Éditions Odile Jacob, 2001. Edition originale : Creating Minds. An Anatomy of Creativity, New York, Basic Books, 1993.
[De Gennes, 1976] ↑ De Gennes Pierre-Gilles, « La percolation : un concept unificateur », in La Recherche, Vol.7 n°72, 976, pp.919-927.
[Jaoui, 1996] ↑ Jaoui H., « La créativité. Mode d’emploi », Paris, ESF Éditeurs, 1996.
[Leleu-Merviel, 2003] ↑ Leleu-Merviel S., « Les désarrois des Maîtres du sens à l’ère du numérique », in H2PTM’03. Hypertextes, hypermédia : Créer du sens à l’ère numérique, Paris, Lavoisier/Hermès Sciences publications, 2003, pp.17-34.
[Leleu-Merviel, 2004] ↑ Leleu-Merviel S., « Effets de la mise en réseau et de la numérisation sur le concept de document », in Revue Internationale I3 : Information, Interaction, Intelligence. A Journal in the Sciences of Information Engineering, Numéro Thématique, Le document numérique, Volume 4 n°1/2004, pp.121-140.
[Lesne, 1996] ↑ Lesne A., « Méthode de renormalisation. Phénomènes critiques, chaos, structures fractales », Paris, Eyrolles Sciences, 1996.
[McClelland, 1995] ↑ McClelland J. L., McNaughton B. et O’Reilly R. C., « Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connexionnist models of learning and memory », in Psychological Review 102, 1995.
[Mugur-Schächter, 2005] ↑ Mugur-Schächter M., « Relativisations descriptionnelles et représentations formelles non-amputées de la complexité », in Intelligence de la complexité : épistémologie et pragmatique, Colloque de Cerisy-la-Salle, Juin 23-30, 2005.
[Nelson, 1981] ↑ Nelson T., « Literary Machines», Mindful Press, 1981.
[Pajot, 2001] ↑
Pajot S., « Percolation et économie», Thèse de doctorat en sciences économiques, Université de Nantes, 2001.
En ligne : http://percolation.free.fr/theseweb004.html#toc1 (consulté le 4 mai 2004.)
[Pavis, 2002] ↑ Pavis P., « Le théâtre contemporain. Analyse des textes, de Sarraute à Vinaver », Paris, Nathan Université, Collection « Lettres Sup. », 2002.
[Ranwez, 1999] ↑
Ranwez S. et Crampes M., « Conceptual documents and hypertext documents are two different forms of Virtual Documents », VD’99. Virtual Documents, Toronto (Canada), 1999.
En ligne : http://www.cs.unibo.it/~fabio/VD99/intro.html (consulté le 5 mai 2002.)
[Rouquette, 1997] ↑ Rouquette M-L., « La créativité », Paris, Presse Universitaires de France, collection « Que sais-je ? », 6 ème édition 1997.
[Wallas, 1926] ↑ Wallas G., « The Art of Thought », New York, Harcourt Brace and World, 1926.
[Zallen, 1983] ↑ Zallen R., « Introduction to percolation: a model for all seasons », in g. Deutscher, r. Zallen, j. Adler (eds) Percolation Structures and Processes, Annals of the Israël Physical Society n°5, Jérusalem, 1983, pp.3-16.