Collection ALS/1992/Forthoffer réseau de neurones
Société des sciences naturelles de Strasbourg //Société des sciences de Nancy // Académie lorraine des sciences |
Apport du réseau de neurones pour une détection de contours par transformée en ondelettes
|
Sommaire
- 1 Avant-propos
- 2 Résumé
- 3 Apport du réseau de neurones pour une détection de contours par transformée en ondelettes
- 4 Voir aussi
Avant-propos
Cette communication est en fait extraite d'un article plus complet, publié dans la revue Traitement du signal (revue) en 1991.
Cette revue est éditée par l'association GRETSI (Groupe de Recherche et d’Études de Traitement du Signal et des Images)[1]
Résumé
 [65]
La méthode présentée dans cet article, constitue un nouvel outil d'extraction des
contours d'une image en niveaux de gris, par coopération de techniques :
décomposition en ondelettes et réseaux neuromimétiques.
[65]
La méthode présentée dans cet article, constitue un nouvel outil d'extraction des
contours d'une image en niveaux de gris, par coopération de techniques :
décomposition en ondelettes et réseaux neuromimétiques.
La première partie est consacrée aux rappels nécessaires quant au formalisme de la décomposition en ondelettes, ainsi que ses principales propriétés.
La phase délicate de l'algorithme réside dans la recomposition optimale des différentes résolutions, afin d'obtenir des contours fins et sans bruit. Cette tâche est avantageusement confiée à un réseau de neurones, objet de la deuxième partie.
L'attrait majeur de cette nouvelle technique, est sa capacité à traiter correctement des images aux caractéristiques très différentes, sans avoir à modifier de paramètres
Abstract
The first part recalls the necessary background on mono and bidimensional wavelet decomposition and their main properties.
The difficult phase of the algorithm lies in the optimal recomposition of different resolutions, in the aim to obtain thin and noiseless edges. This work is given to a neural network which constitutes the object of the second part
The main interest of this new method is to give good results with images whose caracteristics are completly different, without to modify any parameters.
Apport du réseau de neurones pour une détection de contours par transformée en ondelettes
Introduction
La segmentation d'images est une étape pivot entre les phases d'amélioration- restauration et celle de décision. C'est à ce niveau qu'est effectuée une détection, le plus souvent non réversible, de l'information utile dans une image.
Il existe principalement deux approches pour segmenter une image : l'approche par les contours et l'approche par les régions qui lui est duale. Nous nous intéressons ici à l'approche par la détection de contours [10].
Il s'avère que, tenir compte de facteurs perturbateurs tels que le flou ou le bruit apportés lors des phases d'acquisition ou de prises de vues, améliore sensiblement les performances de la détection [4].
La transformée en ondelettes est une analyse multi-échelle permettant une meilleure interprétation du signal et donc des perturbations [3].
La phase de détection de contours réside dans l'extraction des discontinuités de l'image, depuis les différentes échelles. Une solution consiste à combiner les différentes résolutions du signal image, en utilisant un réseau de neurones [12]. Celui-ci est chargé de déterminer une loi de combinaison optimale, face à un critère d'erreur quadratique, calculé pendant la phase d'apprentissage, à l'aide d'une référence déterminée par un expert.
Cette approche originale permet d'appréhender automatiquement, par le biais de l'apprentissage neuronal, le caractère multirésolution de la décomposition en ondelettes.
La transformée en ondelettes
Définitions
Les ondelettes sont des fonctions déterminées par dilatations et translations, à partir d'une fonction appelée ondelette mère. Cette fonction, introduite par Morlet et Grossman [5], permet l'analyse d'un signal.
- (1) avec a>0,
où a est le facteur d'échelle, b le facteur de translation et t le temps.
Pour une analyse temps-échelle efficace, doit être bien localisée en temps et en fréquence. En outre, l'ondelette est assimilée à un filtre passe-haut :
- (2)
Parallèlement à une décomposition en série de Fourier, la transformée en
ondelettes permet de synthétiser un signal en tant que somme de plusieurs
 [68]
ondelettes de facteurs d'échelles variables. Y. Meyer [9], a montré que les
fonctions constituent une base orthogonale de pour et .
[68]
ondelettes de facteurs d'échelles variables. Y. Meyer [9], a montré que les
fonctions constituent une base orthogonale de pour et .
- (3)
Détection de contours par analyse multi-résolution
Transformée en ondelettes sans sous-échantillonnage
Dans la problématique de détection de contours, les informations exploitées sont essentiellement contenues dans les hautes-fréquences, c'est-à-dire les coefficients d'ondelettes . Le sous-échantillonnage matérialisé par l'alternance des "x" et "o" dans la figure 3, provoque la non invariance en translation de la transformée en ondelettes, ce qui entraîne une réponse différente, selon la position de la discontinuité (échantillon pair ou impair).
Pour pallier à ce problème, nous calculons la totalité des échantillons marqués "o" et "x", en intercalant simplement zéros entre les coefficients des filtres h et g qui permettent le passage du niveau de résolution j+1 au niveau de résolution j [3] [6][7].
Coopération "ondelettes-réseau de neurones"
Principe
La recherche d'une loi de composition de toutes ces informations, optimale pour un grand nombre d'images aux caractéristiques très différentes, est donc le point crucial de cette technique. Les difficultés rencontrées dans la recherche de cette loi, nous ont conduits à confier cette tâche à un réseau de neurones, [2], [12].
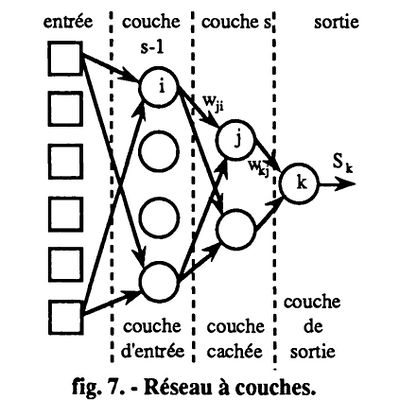
Le modèle utilisé est représenté par la figure 7. Il s'agit d'un réseau à couches, dont l'apprentissage est régi par la règle de rétropropagation du gradient [1].
 [72]
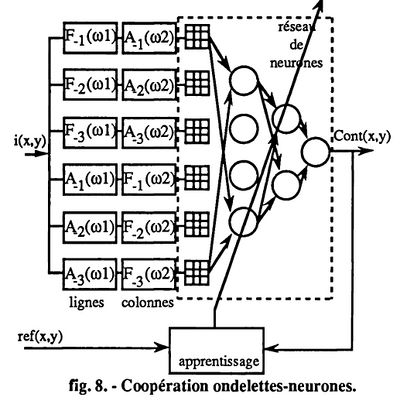
L'interface entre la décomposition en ondelettes et le réseau de neurones est
réalisée en appliquant à chaque neurone de la couche d'entrée, les niveaux des
pixels présents dans chacune des trois résolutions retenues, dans les deux directions
et suivant un voisinage 3 x 3 . Chaque neurone de la couche d'entrée reçoit donc 3
résolutions x 2 directions x 9 pixels, soit un vecteur de 54 composantes.
[72]
L'interface entre la décomposition en ondelettes et le réseau de neurones est
réalisée en appliquant à chaque neurone de la couche d'entrée, les niveaux des
pixels présents dans chacune des trois résolutions retenues, dans les deux directions
et suivant un voisinage 3 x 3 . Chaque neurone de la couche d'entrée reçoit donc 3
résolutions x 2 directions x 9 pixels, soit un vecteur de 54 composantes.
L'algorithme de rétropropagation
Mise en œuvre.
Le réseau de neurones a pour fonction de déterminer si le pixel de coordonnées (x,y) dans l'image d'origine, appartient au tracé d'un contour.
A cet effet, il ne comporte qu'un seul neurone dans sa couche de sortie, et son niveau d'activation doit refléter un degré d'appartenance à une frontière. Pour effectuer ce traitement sur toute l'image, la structure neuronale est appliquée successivement sur tous les pixels des images de la décomposition en ondelettes.
Apprentissage
La rétropropagation du gradient est un algorithme d'apprentissage supervisé, il est donc indispensable de lui fournir une image de référence, modèle du résultat à atteindre. Nous avons à cet effet constitué des leçons, à partir de la banque d'images du GRECO GDR 134-GT8, sur lesquelles nous avons extrait les contours à l'aide de méthodes classiques, adaptées à chacune d'elles.
Après avoir effectué la décomposition en ondelettes d'une image brute, nous présentons successivement chaque pixel de l'image des différentes résolutions à l'entrée du réseau. Celui-ci génère alors une sortie, qui est comparée à la valeur du pixel correspondant dans l'image de référence pour donner l'erreur locale en sortie. Cette erreur est ensuite rétropropagée dans le réseau, afin de modifier chaque poids, ainsi, à chaque itération, la sortie du réseau se rapproche du modèle.
Lorsque l'erreur quadratique globale sur l'image n'évolue plus, l'apprentissage est terminé.
Le but visé étant l'obtention d'un réseau capable de traiter indifféremment et sans modification de réglage, des images de caractéristiques très différentes, la propriété recherchée est la capacité de généralisation.
Pour que le réseau bénéficie de cette propriété, deux conditions principales sont à respecter :
- il faut que les images utilisées lors de l'apprentissage aient des caractéristiques
variées, le lot utilisé est représenté par les figures 11 et 12.
- il faut limiter la connectivité du réseau, sans quoi il serait capable d'apprendre
"par coeur" les leçons, et incapable de traiter correctement une image inconnue.
Utilisation
Lors de l'utilisation, le réseau reçoit en entrée l'image des différentes résolutions de la décomposition en ondelettes. Le réseau se comporte comme un classificateur dont la valeur de sortie définit le tracé des contours
Expérimentations
Afin que le réseau dispose sur ses entrées, d'un maximum d'informations, nous lui injectons une fenêtre de taille 3x3 centrée sur le pixel à classifier, pour chaque résolution. Le seul prétraitement, commun à toutes les images avant la décomposition en ondelette, est un simple rehaussement global.
Dans le but d'obtenir une bonne généralisation du réseau employé, les images brutes et de références sont en fait des agrégats de différentes images, choisies pour leurs disparités de caractéristiques.
La difficulté majeure rencontrée, lors de la mise en oeuvre des réseaux de neurones, est le choix du nombre de couches et du nombre de neurones que comporte chacune d'elles.
Les expérimentations ont montré que si le réseau est trop complexe, il apprend bien mais généralise mal, ce qui nous conduit à rechercher la structure la plus simple possible, capable de donner un résultat satisfaisant.
Le réseau finalement retenu est assez simple, puisqu'il ne comporte que trois couches contenant six neurones dans celle d'entrée, quatre dans la deuxième, et un seul dans celle de sortie.
Cette relative simplicité cache cependant un grand nombre de degrés de liberté représentés par le nombre de liaisons. En effet, utilisant trois résolutions horizontales et trois verticales, reliées à chaque neurone de la couche d'entrée par neuf poids chacune (3x3), nous sommes donc en présence de 9x6x6 = 324 paramètres dans la première couche, 24 dans la deuxième et 4 dans la dernière.
A l'issue de la phase d'apprentissage, dont le rôle est de régler au mieux ces 352 paramètres, le réseau est capable d'extraire les contours à partir des images des différentes résolutions, en éliminant une grande partie du bruit et en complétant même certains contours qui n'apparaissent pas dans le modèle.
Les figures 14 et 15 montrent les résultats obtenus sur les images des figures 11 et 12 appartenant aux leçons apprises.
L'intérêt de la méthode proposée réside dans la capacité à traiter des images étrangères à la banque d'apprentissage. Les résultats atteints dans ce cadre sont très intéressants, comme le montre la figure 16 obtenue en appliquant, sans aucune modification des paramètres, notre algorithme à* l'image de la figure 13
Interprétation
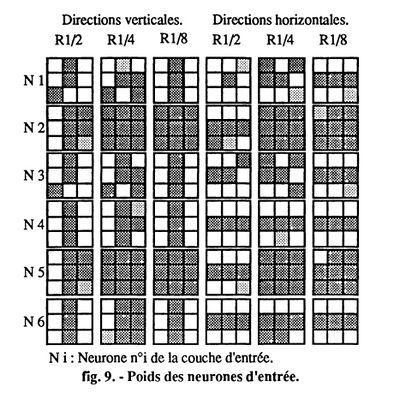
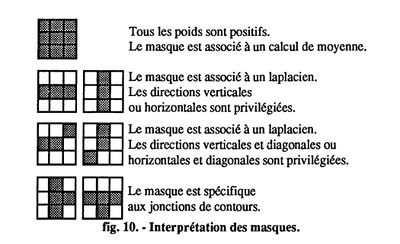
L'interprétation des poids des neurones est délicate. En supposant que tous les poids positifs ou négatifs, sont d'amplitude presque identique nous pouvons alors extraire plusieurs formes typiques de "masques d'entrée", qui sont représentées par la figure 10. Ces informations sont combinées par les couches intermédiaires qui permettent la détection effective des contours.
Certaines configurations des poids en entrée du réseau ont des tâches très spécifiques telles que,
- le calcul de la moyenne qui permet de rehausser le contour ou de le séparer du bruit,
- l'extraction des máxima qui accentue et affine le contour,
- les opérations privilégiant la géométrie des contours (traits, angles, jonctions,...).
Dans l'exemple de la figure 9, les neurones 2 et 5 effectuent sensiblement les mêmes opérations. Un pixel de poids nul a une double interprétation. Il peut indiquer que l'information sur le pixel correspondant n'est sans doute pas représentative du résultat recherché, ou que l'apprentissage n'est pas optimal, c'est- à-dire le plus souvent inachevé. Dans ce cas, la configuration du réseau n'est pas encore celle du chemin idéal recherché entre l'entrée et la sortie du réseau, et on ne peut rien dire sur la pertinence de l'information. Cette dernière hypothèse est la plus probable, la quantité d'informations présentes dans une image, rendant la modélisation d'un tel processus impossible à réaliser de façon exacte. C'est pour cette raison qu'il subsiste toujours quelques configurations de poids d'entrée de réseau, qui ne correspondent à aucune structure classique
Les tâches effectuées par les neurones de la couche cachée et le neurone de sortie sont plus délicates à analyser, mais, à ce stade des expérimentations, nous pouvons supposer qu'ils prennent en compte des notions plus complexes, telles que le bruit ou le flou [4].
Conclusions et perspectives.
La coopération des deux techniques permet d'allier avantageusement d'une part, la représentation complète du signal sous différentes résolutions, fournie par la transformation en ondelettes, et d'autre part le caractère autoréglable des réseaux neuromimétiques, dans la recherche d'une loi de recomposition optimale.
Le principal attrait de cette méthode, contrairement à celles utilisant les gradients ou les laplaciens, est de fournir des contours presque binaires, bien localisés, pour des transitions lentes, rapides ou bruitées, sans avoir de paramètres à ajuster pour chaque situation.
La méthode proposée n'a pas la prétention de devenir un outil universel, mais elle ouvre la voie à d'autres expérimentations dans la recherche de moyens polyvalents de segmentation, en intégrant une phase embryonnaire d'interprétation. Hormis la phase préliminaire d'apprentissage très coûteuse en temps de calculs, l'exploitation de cette méthode peut s'envisager en temps réel avec une architecture pipe-line, dans la mesure où la transformée en ondelettes, comme les réseaux de neurones, peuvent se décomposer en produits de convolution.
Par ailleurs, il reste beaucoup d'expérimentations à faire dans le domaine des ondelettes, comme l'utilisation de décompositions en quinconce. Leur caractère isotrope et non séparable, permet de réduire le nombre de résolutions à étudier, donc a priori les temps de calculs. Cependant, elle nécessite l'emploi d'opérateurs d'ordre supérieur à 2 dont le comportement peut-être plus difficile à exploiter
Bibliographie
[1] ↑ E. DAVALO et P NAIM, "Des réseaux de neurones" - PARIS, EYROLLES, 1990.
[2] ↑ D.J. EVANS & al,, "Searching sets of properties with neural networks" - Parallel Computing, №.16,1990, p. 279-285.
[3] ↑ J.-C.FAUVEAU, "Analyse multi-résolution par ondelettes non orthogonales et bancs de filtres numériques" - Thèse de Doctorat, spécialité informatique, Université de Paris Sud, 1990.
[4] ↑ M. FORTHOFFER, "Détection de contours par transformée en ondelettes et réseaux de neurones" - Thèse de Doctorat, spécialité automatique, Université de Nancy 1,1991.
[5] ↑ A. GROSSMANN & J. MORLET,, "Decomposition of Hardy functions into square integrable wavelets of constant shape" - SIAM J. Math., vol 15, 1984, p. 723-736.
[6] ↑ S.G. MALLAT, "A Theory for Multiresolution Signal Decomposition : The Wavelet Representation" - IEEE Trans, on Pattern Analysis and Machine Intelligence, n°7, July 1989, vol. 11.
[7] ↑ S.G. MALLAT, "Multiresolution representations and wavelets" - Thèse, GRASP Lab, Dept. of computer and information science, Univ of Pennsylvania, 1988.
[8] ↑ P. MATHIEU & al,, "Compression d'images par transformée en ondelette et quantification vectorielle" - Traitement du Signal, Vol 7, n°2,1990.
[9] ↑ Y. MEYER,, "Principe d'incertitude, bases hilbertiennnes et algèbre d'opérateurs" - Séminaire Bourbaki n°662,1985-86.
[10] ↑ O. MONGA,, "segmentation d'images : où en sommes nous ?" - rapport de recherche INRIA-Rocquencourt, №1216, support de cours pour le congrès PIXIM 89,1990.
[11] ↑ M J. SMITH and D.P. BARNWELL,, Exact reconstruction for tree-structured subband coders. IEEE Trans, on ASSP 34,1986, p.434-441.
[12] ↑ P. J. WERBOS, "Backpropagation through time: what it does and how to do it" - Proceedings of the IEEE, № 10, October 1990, vol. 78.
Voir aussi
- Dans le réseau Wicri :
La page de référence « Collection ALS/1992/Forthoffer réseau de neurones » est sur le wiki Wicri/Académies Grand Est.
- ↑ Le GRETSI offre ses articles publiés avant 2017 (à la date de rédaction de cet article) en libre accès.