CIDE (2009) Charbonneau

Le recours à des environnements numériques pour documenter le patrimoine bâti : une approche basée sur la complémentarité entre photogrammétrie et objet paramétrique

---

 
 

titre Le recours à des environnements numériques pour documenter le patrimoine bâti : une approche basée sur la complémentarité entre photogrammétrie et objet paramétrique auteurs Nathalie Charbonneau et Pierre Grussenmeyer. nathalie.charbonneau@umontreal.ca pierre.grussenmeyer@insa-strasbourg.fr Affiliations UMR MAP 694, Équipe PAGE, INSA de Strasbourg, France In CIDE.12 (Montréal), 2009 En PDF  CIDE (2009) Charbonneau.pdf Mots-clés  Patrimoine bâti, photogrammétrie, librairie de composants, objets paramétriques, programmation 3D, ouvertures. Keywords Built heritage, photogrammetry, component library, parametrical object, 3D programming, openings.

Résumé

Cet article expose une méthode qui a été développée afin de tirer profit de la complémentarité pouvant exister entre objet paramétriques et photogrammétrie, dans le cadre de projets de restitution architecturale. Nous explorons la possibilité d’élaborer la maquette numérique d’un artéfact par le biais d’un processus en trois étapes; i) d’abord sélectionner de façon interactive le type des composants, ii) ensuite, effectuer une mise à l’échelle automatique à partir d’un nuage de points de base densité et finalement iii) effectuer les retouches nécessaires pour adapter la topologie de l’objet virtuel au cas de figure observé. Pour ce faire, nous avons développé un environnement numérique faisant appel aux applications Maya 1 et Photomodeler 2 . Notre étude de cas porte sur les détails architecturaux composant les ouvertures dans les façades de bâtiments résidentiels. Nous retraçons la démarche de restitution à partir d’un exemple de fenêtre à guillotine dont la configuration est typique du patrimoine bâti montréalais.

English description

Abstract 

This paper describes the methodology of an ongoing research project concerned with the possibility of making use of parametrical objects and photogrammetric techniques within the framework of an architectural restitution project. We explore the possibilities of elaborating the 3D model of an artefact by means of a three steps procedure: i) select the components’ type in an iterative way, ii) put to scale the resulting model, automatically retrieving the relevant data from a points cloud and iii) retouching the model in order to adapt the object topology to the scenario under study. With this in view, we implement a digital environment making use of the following commercial software: Maya1 and Photomodeler2. Our case study deals with architectural details adorning openings in residential buildings. By way of example, we describe the restitution process of a sash window, typical of the Montreal built heritage.

 

Introduction

Le but d’un projet de restitution architecturale est habituellement de documenter un élément patrimonial et de présenter l’information tridimensionnelle de façon conviviale, afin de permettre l’extraction de données pertinentes par différentes catégories d’intervenants. Dans cette optique, le bâtiment (ou l’ensemble architectural) est modélisé afin de générer une maquette numérique. Dans le cadre du présent exposé, nous portons notre intérêt sur l’une des facettes du travail du modélisateur, soit la restitution des détails architecturaux. Pour documenter les éléments appartenant au patrimoine bâti, les technologies numériques offrent une vaste panoplie de solutions. Dans nombre de projets de restitution, on a recours aux outils de dessin de logiciels CAD pour élaborer la maquette numérique de bâtiments. Il est cependant notable que, lorsqu’il s’agit de modéliser certains éléments, tels que les détails architecturaux, développer un modèle géométrique distinct correspondant à chacun des cas de figure existant peut constituer un véritable ‘travail de moine’, dépendamment de l’ampleur du projet. Au cours des dernières années, plusieurs stratégies alternatives ont été développées par les chercheurs, pour pallier à ce problème. L’objet paramétrique est celle qui retient ici notre intérêt ; il s’agit d’une stratégie basée sur le concept de modules réutilisables. En effet, ce type d’approche permet de transformer la configuration d’un objet en modifiant de manière interactive les valeurs numériques associées aux paramètres. Dans le cadre de projets de restitution, les objets paramétriques, auxquels on a attribué les valeurs qui convenaient, sont ensuite insérés dans la maquette du bâtiment que l’on cherche à restituer. Une librairie d’objets interactifs peut contribuer à optimiser le travail du modélisateur, ce qui se traduit par un considérable gain de temps. Le lecteur trouvera un exemple de ce type d’approche sur le site GOP qui présente les travaux menés par le CRAI [1].

Pour attribuer aux différents paramètres les valeurs qui conviennent, il faut nécessairement connaître les dimensions de l’objet réel. Or, arriver à connaître les dimensions d’un élément architectural peut poser problème selon l’accessibilité de cet objet. Dans le cas des ouvertures, il arrive qu’on doive effectuer toute une série de mesures fines sur des détails situés en hauteur. Par ailleurs, il arrive qu’on doive mesurer à maintes reprises des éléments semblables (linteaux, appui, petits bois, etc.) sur des ouvertures de même type ou de types similaires. Ces problèmes peuvent ralentir, voire entraver, le déroulement des travaux de restitution numérique. C’est pourquoi nous cherchons à proposer une méthode visant d’une part à augmenter ce que l’on pourrait appeler ‘l’accessibilité virtuelle’ de l’objet et, d’autre part, visant à systématiser la façon de consigner les caractéristiques de l’objet et d’effectuer les relevés. Un paramètre important dans la définition d’une méthodologie de relevé, et dans le choix d’une technologie, est le niveau de complexité de l’objet [2]. Notre étude de cas sur les ouvertures dans les bâtiments résidentiels nous amène à analyser des objets d’une géométrie relativement peu complexes, mais dont les différentes ‘instances’ sont déclinées avec de multiples variations. Le peu de complexité de ces objets découle du fait qu’un ensemble relativement restreint de primitives géométriques et de dimensions suffisent habituellement à en décrire la géométrie. Pour un type donné d’ouverture, ces dimensions forment un ensemble que l’on peut définir a priori (largeur et hauteur de l’ouverture, largeur et hauteur du linteau, etc.). Dans ce contexte, il est permis de présumer que le recours à l’objet paramétrique pour consigner les caractéristiques de l’objet, ainsi que l’utilisation de nuages de points pour extraire les données numériques nécessaires, pourrait optimiser la démarche du modélisateur. Nos travaux reposent sur la possibilité de combiner les avantages de ces deux méthodes, soit la flexibilité de l’objet paramétrique et la précision, en termes de dimensionnement, propre à l’application de techniques de photogrammétrie. Dans cette optique, nous avons développé un environnement numérique faisant tour à tour appel à deux applications, Maya et Photomodeler , la première pour le développement d’algorithmes rendant possible l’élaboration d’objets paramétriques, la seconde pour permettre le recours aux techniques de photogrammétrie . Au cours de l’exposé qui suit, nous retraçons la démarche qui nous a permis de combiner le potentiel de deux approches distinctes mais complémentaires. À partir d’un exemple concret (la génération de la maquette numérique d’une fenêtre), nous expliquons de quelles façons les données sont saisies, traitées et exploitées. Cette démarche, qui est présentée au cours des prochaines sections, se déroule en trois phases, soit la sélection des composants, la mise à l’échelle automatique et les modifications finales.

Première étape : la sélection des composants

Nous travaillons depuis plusieurs années à formaliser, par le biais d’algorithmes, la logique de composition d’artéfacts appartenant au patrimoine bâti [3]. En nous référant à une typologie donnée, l’expertise développée nous permet maintenant de décrire des ensembles de cas de figure sous forme de modèles fédérateurs. Ceux-ci ont pour mandat de permettre la génération (semi-automatique) de maquettes numériques représentant un maximum de cas de figure divers, mais inter-reliés au niveau formel. Ce type d’approche offre la possibilité de développer des objets paramétriques avec lesquels l’utilisateur interagira par le biais d’interfaces graphiques. Le mandat de cette interface est de permettre à l’utilisateur de sélectionner les différents composants (et type d’organisation) de l’artéfact et de transmettre ces informations au système qui, lui, génèrera le modèle 3D.

Figure 1. Fenêtre à guillotine

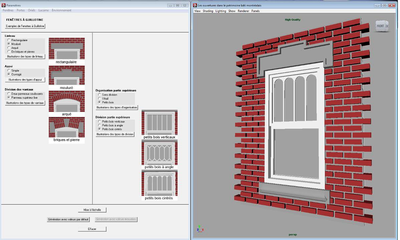
Nous appliquons maintenant cette approche au processus de restitution architecturale. Dans le cadre de la démarche que nous retraçons, les ouvertures du bâtiment sont restituées en tant qu’entités autonomes. Dans cette logique, les maquettes partielles, représentant les diverses ouvertures, seront ultérieurement insérées dans la maquette globale du bâtiment. L’artéfact que nous utilisons pour exposer ce processus est une fenêtre à guillotine (voir figure 1). Il s’agit là d’un type d’ouverture couramment employé dans les habitations montréalaises de type duplex ou triplex construites au début du XXème siècle.Pour reconstituer la géométrie de cet artéfact, la première phase en est une d’observation. L’utilisateur doit sélectionner les différents composants et transmettre ces informations au système par le biais de l’interface graphique. Pour le développement de cette dernière, nous avons eu recours au langage MEL (Maya Embedded Language). Nous avons privilégié le paramètre de type non numérique et opté pour un mode de contrôle offrant la possibilité de choisir de façon itérative entre diverses options mutuellement exclusive. Les différentes alternatives proposées sont illustrées de façon schématique dans l’interface à proximité de radio buttons. Ceux-ci permettent à l’utilisateur de sélectionner de façon conviviale les différents composants de l’objet à restituer (voir figure 2).

Figure 2. Interface basée sur des radio-buttons

Par le biais de ces ensembles de radio-buttons, l’utilisateur sélectionne les valeurs (non-numériques) qu’il convient d’assigner aux différents paramètres, à savoir le type de linteau, le type d’appui, le type d’organisation des petits bois, etc. L’utilisateur est en mesure d’amalgamer différents types de composants pour arriver à une configuration qui soit, le plus possible, en conformité avec la réalité observée. Au terme de cette étape, la maquette 3D de l’artéfact est générée par l’environnement Maya en utilisant les dimensions par défaut. L’utilisateur peut alors évaluer la maquette résultante, afin de vérifier la conformité de la configuration avec l’artéfact à l’étude (au niveau des types de composant). Cet examen visuel pourra révéler quelques disparités entre le modèle et l’artéfact. Nous reviendrons sur cette éventualité dans la troisième partie de l’exposé.

Deuxième étape : la mise à l’échelle

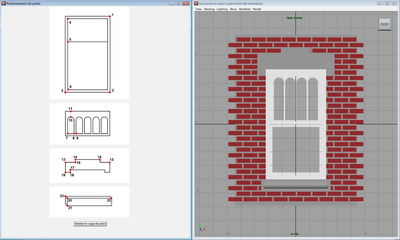
Suite à la phase d’observation et de sélection des composants, on passe maintenant à l’étape de mise à l’échelle, qui mettra à contribution les techniques de photogrammétrie. À partir du moment où tous les paramètres ont été déterminés, l’utilisateur a accès à l’option ‘Générer un nuage de points’. Cette dernière, lorsqu’activée, entraîne l’apparition d’une nouvelle fenêtre présentant de façon graphique la stratégie à adopter pour élaborer le nuage de points en question. La stratégie recommandée différera selon le cas de figure sur lequel travaille l’utilisateur. En d’autres termes, pour chacun des composants sélectionnés précédemment, un croquis démontre quels points devront être référenciés ainsi que la nomenclature appropriée.

Figure 3. Illustrations démontrant la stratégie à adopter pour élaborer le nuage de points

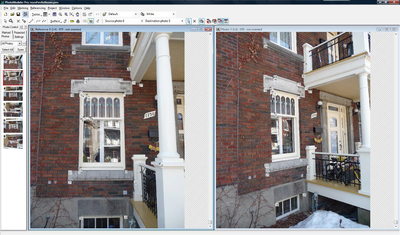
L’utilisateur pourra se référer à ces croquis tout au long du processus d’élaboration du nuage de points. Au moment jugé opportun par l’utilisateur, l’application Photomodeler est activée à partir de l’interface principale. Comme nous le savons, ce logiciel permet de générer des nuages de points à partir de plusieurs photographies d’un même objet, prises sous des angles de vue qui diffèrent. L’utilisateur sera appelé à sélectionner les photographies de l’artéfact sur lesquelles il souhaite travailler. Il s’agira pour lui d’identifier chacun des points apparaissant sur les croquis, et ce, sur les différentes photographies .

Figure 4. Le nuage de points référencés dans l’application Photomodeler

L’aspect sémantique est ici crucial. En effet, chacun des points doit être identifié et nommé conformément aux croquis et consignes fournies dans l’interface principale. Par exemple, dans le cas de la fenêtre à guillotine, les points #1 à #3 sont utilisés pour consigner la position des sommets délimitant l’ouverture; le point #1, le sommet supérieur droit du rectangle formant l’ouverture, le point #2 le sommet inférieur droit, le point #3 le sommet inférieur gauche et ainsi de suite… Le respect de la nomenclature est de toute première importance puisque, par la suite, les points #1 et #2 seront automatiquement utilisés pour calculer la hauteur de l’ouverture, les points #2 et #3, la largeur, etc. Dans notre exemple, les points #4 à #6 sont utilisés pour consigner les dimensions des panneaux, les points #7 à #11, les dimensions des petits bois, les points #12 à #19, les dimensions du linteau et les points #20 à #23, les dimensions de l’appui. Notons que, quel que soit l’élément architectural à l’étude, il est toujours important de référencer également quelques points (ici #24 à #30) répartis sur le reste de la façade afin d’optimiser les calculs effectués par le système pour le positionnement des points dans un espace tridimensionnel. Il est par ailleurs possible d’effectuer des vérifications durant l’élaboration du nuage de points ; on pourra alors s’assurer que certains points sont colinéaires ou que les axes définis par quatre points sont perpendiculaires, conformément à la logique du modèle.

Le nuage de points ainsi constitué est un nuage de base densité puisqu’il compte tout au plus une trentaine de points. Lorsque l’utilisateur a terminé de référencer tous les points utiles, le nuage de points est exporté sous forme de fichier script en langage MEL, cette fonctionnalité étant disponible dans le sous-menu ‘Export model’ du logiciel Photomodeler. Chaque point identifié est alors considéré comme un locator, c’est-à-dire un repère dans l’espace tridimensionnel. Les locators se voient automatiquement attribuer les mêmes noms que ceux qui ont été donnés dans Photomodeler; le point #1 devient le "locator1" et ainsi de suite... Sous Maya, chaque entité existant dans l’espace tridimensionnel d’une scène est liée à un nœud transform par la relation enfant/parent; il s’agit de graphes directionnels acycliques (ou DAG nodes). Ce nœud transform reçoit un nom et des attributs; il gère les transformations de l’entité, soit sa position, son orientation et sa taille. (Pour plus d’informations sur les DAG nodes, voir Gould [4 ]). Le script qui est exporté vers Maya établit les liens entre transforms et locators. Pour les points #1 et #2 de notre exemple, la relation est formalisée de la façon suivante :

createNode transform -n "locator1";

setAttr ".t" -type "double3" -0.811823 0.399546 -4.26539;

createNode locator -n "locatorShape1" -p "locator1";

setAttr -k off ".v";

createNode transform -n "locator2";

setAttr ".t" -type "double3" 1.03848 0.410492 -3.95695;

createNode locator -n "locatorShape2" -p "locator2";

setAttr -k off ".v";

Lorsque le fichier texte est importé dans l’environnement numérique principal, chacun de ces transforms est interrogé, de façon à récupérer la position en x, y et z des différents locators. Les diverses coordonnées sont ensuite transformées en vecteurs, afin de rendre ces données exploitables sous MEL.

float	= `getAtt	$p1x	locator1.translateX`;
float	= `getAtt	$p1y	locator1.translateY`;
float	= `getAtt	$p1z	locator1.translateZ`;

vector $v1 = <<$p1x, $p1y, $p1z >>; // le sommet supérieur droit du rectangle formant l’ouverture

float $p2x = `getAttr locator2.translateX`;

float $p2y = `getAttr locator2.translateY`;

float $p2z= `getAttr locator2.translateZ`;

vector $v2 = <<$p2x, $p2y, $p2z >>;// le sommet inférieur droit du rectangle formant l’ouverture

Une fois les données transformées, il s’agit de soustraire un vecteur de l’autre afin d’obtenir la longueur du vecteur résultant. Cette valeur correspond à la distance entre les deux points traités. Pour chacun des couples de points pertinents, ces opérations se font automatiquement, sans que l’utilisateur ne soit impliqué dans le processus.

vector $vResultant = $v1 - $v2;

float $hauteur = mag ( $vResultant ); //la hauteur de l’ouverture

Les distances entre chacun des couples de points constituent un ensemble de proportions : par exemple la proportion entre la hauteur et la largeur du linteau, la proportion entre la largeur des petits bois et leur espacement, etc. Pour effectuer la mise à l’échelle à proprement parler, il faut nécessairement avoir mesuré au moins une distance. Dans l’exemple qui nous occupe, la base de l’ouverture a été mesurée (1.085 m). Cette valeur a été assignée à l’espacement existant entre les points #2 et #3, dans l’application Photomodeler, suite au positionnement des différents points. Si, en raison de l’inaccessibilité de l’objet, il est impossible d’effectuer cette mesure, il est parfois envisageable de l’évaluer, notamment dans le cas d’une ouverture perçant un mur de briques. En effet, la largeur de l’ouverture varie habituellement entre 3 et 5 briques (3, 3½, 4, 4½, 5). La dimension des briques étant standard (20.5 x 6 cm) il est possible de déduire la valeur de la base de l’ouverture (l’épaisseur du mortier étant évaluée à 1cm). Cette dimension (mesurée ou déduite) étant connue, le système est en mesure de déduire toutes les autres. Voici une liste de toutes les distances extraites à partir du nuage de points de notre exemple :

Pour l’ouverture :

• • hauteur et largeur,
  • hauteur du panneau supérieur,
  • hauteur du panneau inférieur,
  • largeur, espacement et décalage vertical des petits bois,

Pour le linteau :

• • hauteur et largeur de l’élément,
  • hauteur et largeur du redent supérieur,
  • hauteur et largeur du redent inférieur,

Pour l’appui:

• • hauteur, largeur et profondeur de l’élément.

Il est important d’établir, dès le début de l’élaboration du système, le niveau de détail recherché. Dans notre exemple, nous prenons le parti de nous restreindre à une quinzaine de dimensions extraites à partir du nuage de points. Les valeurs attribuées au détail fin, telles que dimension des moulures, largeur du châssis et du cadre (etc.) sont attribuées par défaut. Cependant, dans le cas d’une ouverture très ouvragée, le détail fin (tel que les moulures et bas-reliefs) pourra être pris en considération dans la mesure où il aura été possible de s’approcher de l’objet pour le photographier. Ceci étant dit, il est évident que le niveau de détail requis est intimement lié à la finalité du modèle.

Suite aux calculs, un algorithme effectue des vérifications pour évaluer la cohérence des données extraites à partir du nuage de points; il pourra déceler certaines incongruités dans la logique constructive. Dans notre exemple, le système déduit que la hauteur de l’ouverture fait 1.762 m. Or, dans un cas comme celui d’une ouverture perçant un mur de brique, il faut prendre en considération la question du calepinage. Lorsque l’ouverture est générée avec les dimensions par défaut, la hauteur de l’ouverture est calculé par l’expression suivante (int * ($hauteurBrique +$hauteurMortier)) dans laquelle "int" est un entier représentant le nombre de rangs de briques. Lorsque la valeur déterminé par le système pour la hauteur de la fenêtre ne correspond pas à un nombre entier de rangs de briques, on peut en déduire qu’il y a imprécision, soit dans l’estimé de la dimension de la brique, soit dans le nuage de points. Dans notre exemple, la fenêtre ferait 25.18 briques de hauteur, ce qui est improbable. Le système arrondira cette valeur à l’entier le plus près (25) et, le cas échéant, ajustera la hauteur des panneaux en conséquence, tout en respectant les ratios. (Notons qu’ici la dimension standard de la brique ne sera jamais réajustée afin de préserver la cohérence au niveau de la façade dans son entièreté.)

Un autre type d’erreur peut surgir si la nomenclature n’a pas été respectée. Le système détecterait par exemple que l’espacement entre les petits bois est inférieur à la largeur de ceux-ci, ou encore que la largeur du redent est supérieur à la largeur totale du linteau. L’algorithme effectue donc un ensemble de vérifications. En cas d’anomalie, soit il procède automatiquement à des rectifications afin que l’output soit cohérent, soit il affiche un message indiquant que des erreurs ou des imprécisions peuvent remettre en cause la validité du modèle généré.

En somme, les valeurs non numériques assignées par l’utilisateur ont un impact sur le type de nuage de points qui sera requis. L’analyse de ce nuage de points, quant à elle, permet d’assigner automatiquement les valeurs numériques aux dimensions. Par la suite, ces données sont traitées par l’algorithme en vue de déceler des anomalies. C’est le flux de l’information à travers les procédures conditionnelles qui fait la richesse d’une telle approche, basée sur le recours conjoint à la photogrammétrie et à la programmation fonctionnelle. Les mécanismes de vérification inclus dans l’algorithme permettent de valider (ou invalider partiellement selon le cas) les valeurs numériques générées automatiquement à partir du nuage de points. Bref, il s’agit de coller le plus possible à la réalité physique dont rend compte le nuage de points, et ce, tout en respectant la logique des principes de composition de l’artéfact. Au terme du traitement des données extraites du nuage de points, l’utilisateur a accès à l’option ‘Mettre à l’échelle’. L’activation de cette option provoque l’affichage, dans l’environnement Maya, de la maquette numérique résultante.

Figure 5. Saisie d’écran du modèle 3D à l’échelle

Troisième étape : les modifications et l’insertion

On peut supposer que, dans une majorité de cas, il sera nécessaire d’effectuer certains ajustements et de modifier légèrement la topologie de l’élément, afin de rendre le modèle plus conforme à la réalité. Lorsque les types de composants disponibles dans l’environnement numérique ne correspondent pas exactement ce dont l’utilisateur a besoin, deux pistes sont envisageables :

(i) À la fin du processus de restitution, l’utilisateur pourra procéder à des manipulations manuelles, dans l’environnement Maya, pour modifier la topologie de l’objet ; il y aura ajout, retrait ou modification de certains éléments et détails.

(ii) Si le projet de restitution se fait en parallèle avec la démarche de recherche, le prototype d’environnement numérique pourra évoluer à mesure que le programmeur remaniera cet environnement pour y inclure un plus grand nombre de types et de cas de figures.

Au terme du processus de restitution de l’artéfact, et après avoir fait les ajustements nécessaires, il sera possible d’insérer cet élément, ici l’ouverture, dans la maquette du bâtiment complet (et éventuellement d’insérer cette dernière dans la maquette d’un ensemble architectural).

Figure 6. Maquette numérique de la façade d’une habitation de type duplex dans laquelle a été insérée l’ouverture

Conclusion

Dans le cadre d’un projet de restitution architecturale, une approche de ce type peut contribuer à optimiser la démarche du modélisateur dans la mesure où l’on arrive à identifier un leitmotiv dans la trame architecturale. Le cadre bâti à restituer doit être caractérisé par la récurrence de certains éléments dont les différentes ‘instances’ sont déclinées avec de multiples variations. Le modélisateur devra établir une typologie de ces éléments architecturaux en fonction des travaux à effectuer et de l’ensemble architectural à l’étude. De plus, la librairie élaborée à partir de cette typologie devra contenir un bon nombre d’objets paramétriques et chacun de ceux-ci couvrir une gamme relativement vaste de cas de figure. Cette diversité est essentielle. En effet, lorsque le modélisateur aura recours à ce type de système, plus il se verra contraint de retoucher la géométrie de l’objet, plus la pratique nous éloignera du principe du module réutilisable à la base de ce type d’approche.

Notons en outre que, pour optimiser la performance d’un tel système, il semblerait préférable de travailler dans un premier temps uniquement sur des éléments architecturaux clairement définis (tels qu’ouvertures, corniches, pilastres, etc.) et non sur une façade ou un bâtiment dans son entièreté. D’une part, il est plus difficile d’élaborer une typologie de façade en raison de la multiplicité des cas de figure. D’autre part, étant donné que l’aspect sémantique est crucial, il est important que le nuage de points demeure de base densité. Si la densité venait à augmenter au- delà d’une certaine limite (une centaine de points par exemple), le nuage pourrait devenir difficile à gérer par l’utilisateur.

Il est clair que l’élaboration d’un tel système – typologie, objets paramétriques, interface – demande un investissement de temps non négligeable. Cependant, s’il s’agit de restituer un ensemble de bâtiments dans lequel on décèle une homogénéité relative de la forme architecturale, ce type d’approche pourra porter fruit. Il faut cependant demeurer conscient du fait que le gain de temps réel ne pourra être évalué qu’en comparant la méthode ‘traditionnelle’ (impliquant le recours aux fonctionnalités des logiciels CAD) et la méthode proposée. Ce gain pourrait croître proportionnellement au développement du système; plus ce dernier est étoffé (en termes de types d’ouvertures et de types de composants), plus il y aurait théoriquement optimisation du processus de restitution numérique. Seule la mise à l’essai d’un tel système, sur divers projets de restitution portant sur un cadre bâti relativement homogène, pourra nous renseigner sur l’efficacité de l’approche proposée.

Remerciements : Nous remercions le Fonds Québécois de Recherche sur la Société et la Culture (FQRSC), qui a subventionné ce projet de recherche dans le cadre du programme de Bourse de Recherche Postdoctorale.

Références bibliographiques

[1] ↑ Chevrier, C. et Perrin, J.P. (2009). Generation of architectural parametric components, Proceedings of CAAD future 2009, Montréal, June 17-19, pp. 1005-118.

[2] ↑ Grussenmeyer, P. (2008). Photogrammétrie et lasergrammétrie pour la documentation du patrimoine culturel. In Patrimoine et Enjeux, p. 15-34. Paris : Europia Productions.

[3] ↑ Charbonneau, N., Boulerice D. et Booth, D. (2006). Understanding Gothic Rose Windows with Computer-Aided Technologies. Actes de la conférence eCAADe24, Volos, p.770-777.

[4] ↑ Gould, A. D. (2002). Complete maya programming. San Francisco: Morgan Kaufmann.[4] Gould, A. D. (2002). Complete maya programming. San Francisco: Morgan Kaufmann.

Notes